Divide and Conquer Paradigm in Algorithms

Divide and Conquer paradigm is a way to design algorithms that solve problems in such a way that the problem is broken down into one or more smaller instances of the same problem and each smaller instance is solved recursively. These smaller instances of the bigger problem are called subproblems. We keep on breaking the subproblems to a level at which we can solve them directly. Then the solutions of these subproblems are combined to get the solution for the main problem. There are mainly three steps in a divide and conquer algorithm —

Divide — The problem is broken down or divided into a number of subproblems that are smaller instances of the same problem.
Conquer — The subproblems are solved recursively. If the subproblem sizes are small enough , however, just solve them in a straightforward manner.
Combine — The solution to the subproblems are combined to get the solution for the main problem.

Depending upon the size of the subproblem, there are two cases —

Recursive case — Subproblem size are large enough and they have to be solved recursively.
Base case — Subproblem size are small enough such that they can be solved directly and we do not need to recurse.

Recurrences

A recurrence is an equation or inequality that describes a function in terms of it’s value on smaller inputs. In our case, mainly they will be used to denote the running time of algorithms. For example, this is the recurrence for the running time of Merge-Sort.

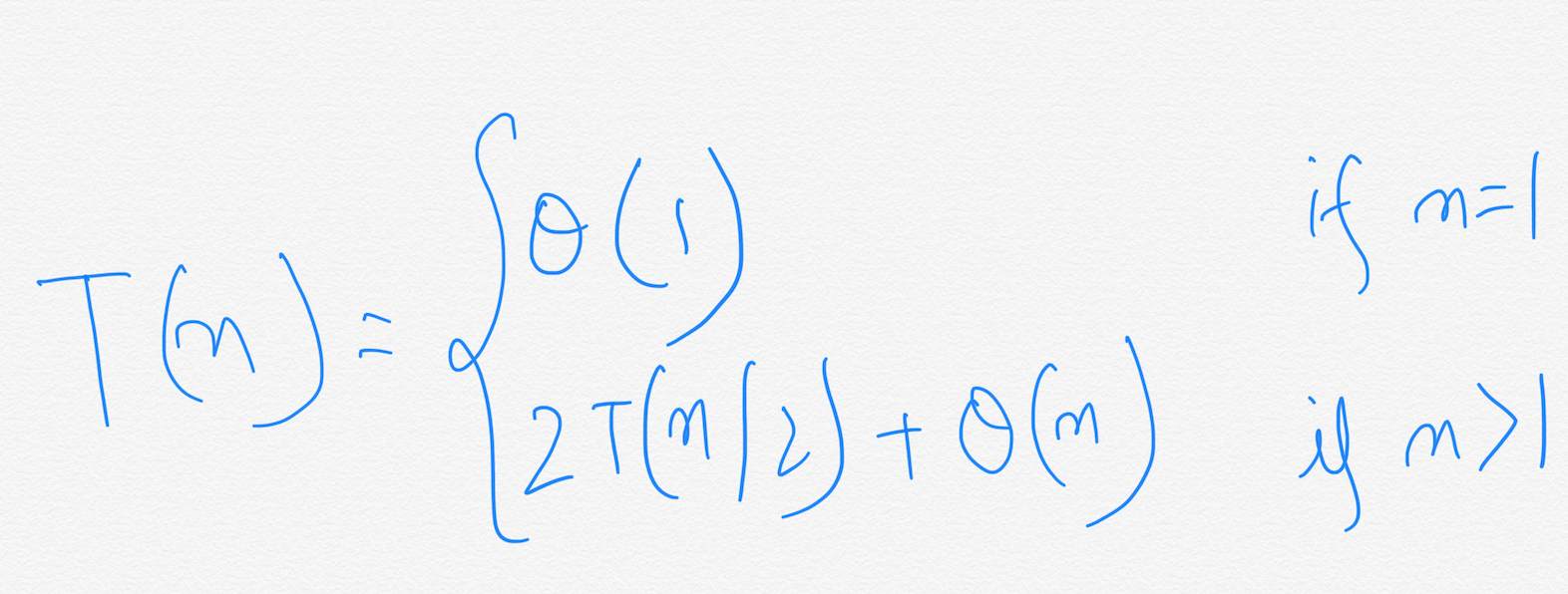
There are three methods for solving recurrences of these types. That is, for obtaining asymptotic Theta(⍬) or Big-oh(O) bounds on the solution. They are,

Substitution method.
Recursion tree method.
The Master method.

We will see all these methods in detail in other articles. In this article, we are going to use Recursion tree method to solve the recurrence. Next, we will see an example in which we will use Divide and Conquer technique to design an algorithm that solves a problem. This problem is called The Maximum-Subarray problem.

The Maximum-Subarray problem.

We will use a real life example to get to the maximum-subarray problem. Consider yourself as a investor. You buy and sell stocks to earn maximum profit from it. Now,

You are given Stock prices of a company.
You are allowed to buy one unit of stock at a time and then sell it at a later date.
Buying and selling are done after the close of trading for the day.
You know what the prices will be in the future.
Your goal is to maximise the profit.

Lets take a problem with some some stock prices.

We are given the prices at the end of each day. Price at Day 0 denotes the price before beginning of Day 1. How will we approach solving this problem ?

You might think that to get maximum profit, buy at the lowest price and sell at the highest price. But this may not be always possible since the highest price may occur at a date before the date at which the lowest price occurs.

The easiest method to solve this problem is to get the profit for each pair of buy and sell dates in which the buy date precedes the sell date. A period of n days has C(n,2) such pair of dates.

We know that C(n,2) = ⍬(n²)

The best we can hope for is to evaluate each pair of dates in constant time. This approach will take Ω(n²) time.

A transformation.

Instead of looking at the daily prices, let us instead consider the daily change in price, where the change on day *i *is the difference between the prices after day ***i-1 ***and after day i.

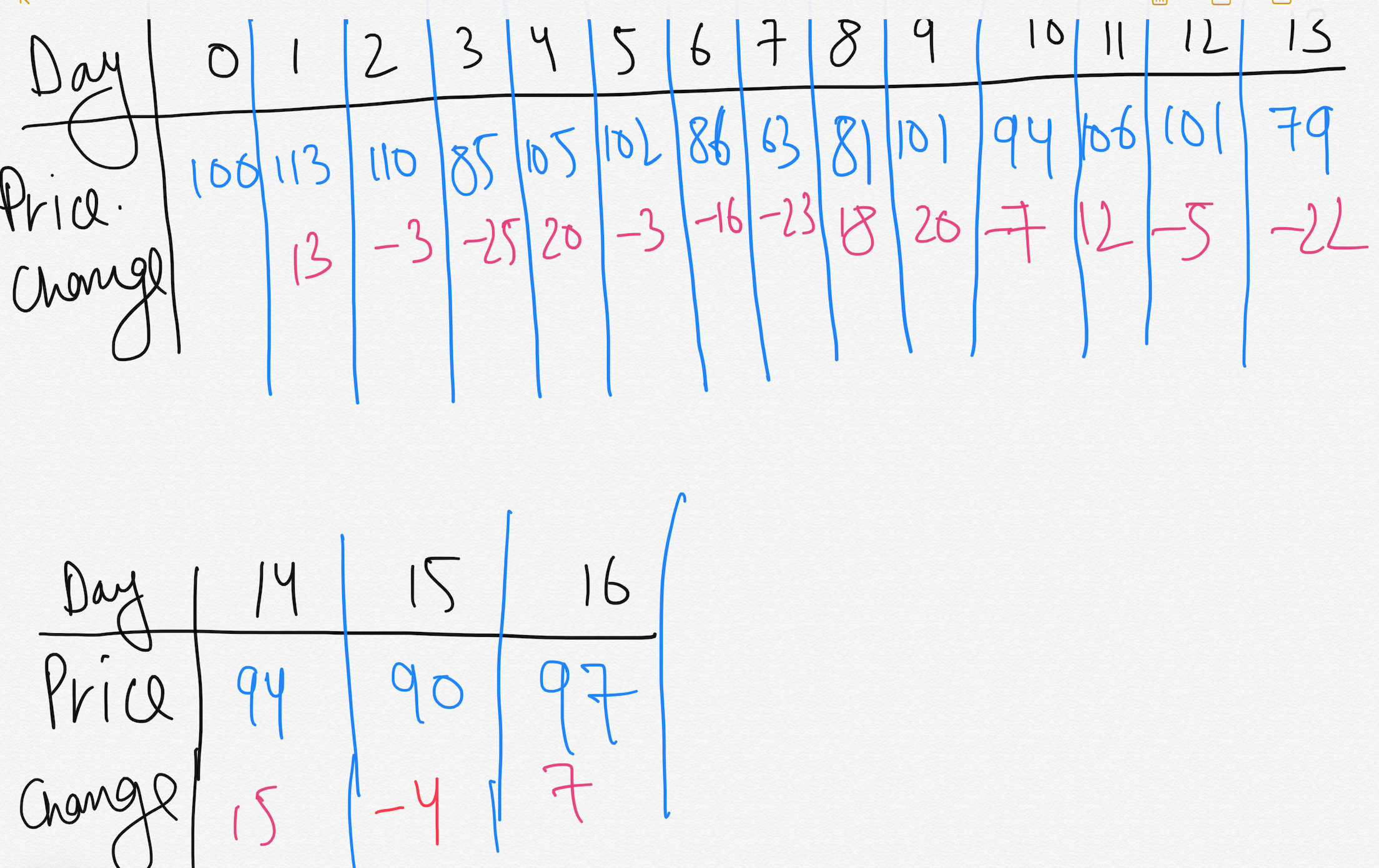
So now lets take the changes value in an array A —

We now want to find a non-empty contiguous subarray of A whose values have the largest sum. We call this contiguous subarray the Maximum Subarray.

Example, the maximum subarray of A[1…16] is A[8…11] with sum 43. Thus, you would want to buy the stock just before day 8(i.e. after day 7) and sell it after day 11, earning a profit of $43 per share.

We can think that this transformation still does not help. We need to check C(n-1, 2) = ⍬(n²) subarrays for a period of n days. By optimisation , this approach again takes ⍬(n²) time which is no better than the Brute-force solution. Can we do better ?

A solution using Divide and Conquer

Suppose, we want to find a maximum subarray of a subarray A[low….high]. Divide and Conquer suggests that we divide the subarray into two subarrays of as equal size as possible.

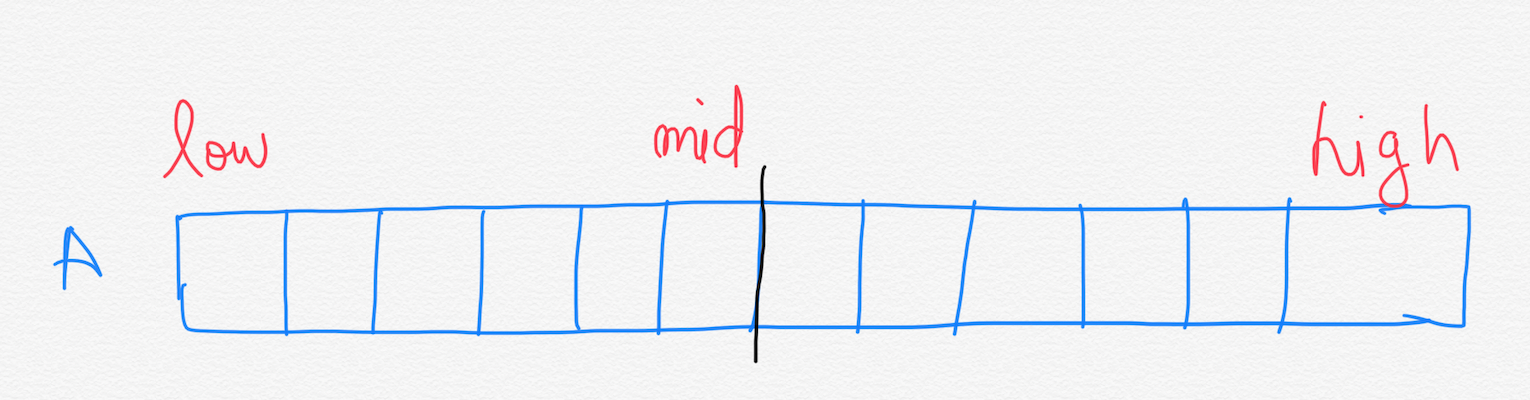
We now have two subarrays A[low….mid] and A[mid+1….high].

The Maximum Subarray can lie in one of these three areas —

Entirely in A[low….mid]
Entirely in A[mid+1….high]
Crossing the midpoint mid

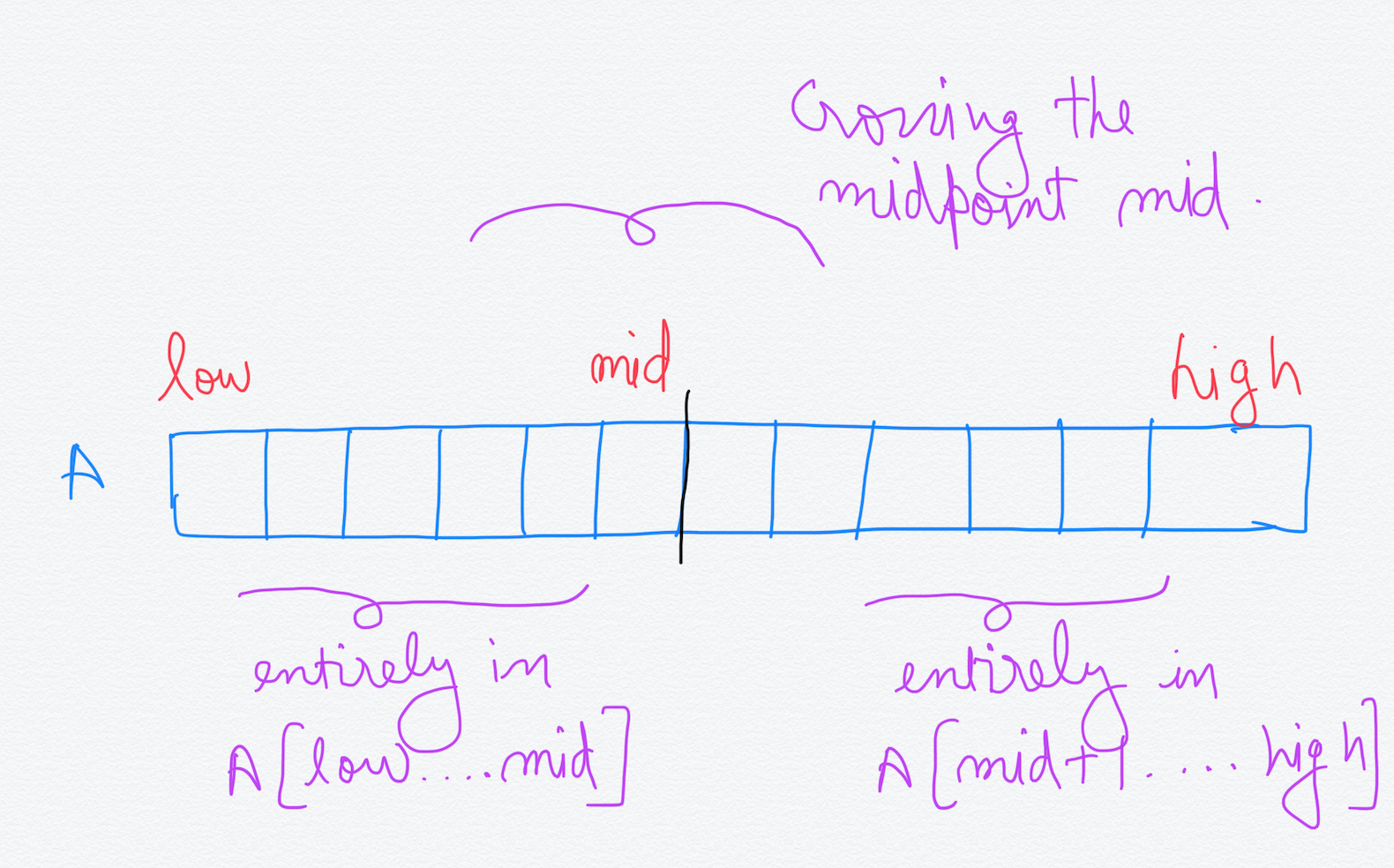
We can see that the first two cases above are smaller instances of finding the Maximum Subarray in the entire array. Also, the Maximum Subarray of the entire array A[low….high] will be the one with maximum sum out of these three. But first we need to write the pseudo-code to find the Maximum Subarray that crosses the midpoint mid.

FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high)
    
    left-sum = -⚮
    sum = 0
    for i = mid downto low
        sum = sum + A[i]
        if sum > left-sum
            left-sum = sum
            max-left = i

    right-sum = -⚮
        sum = 0
        for j = mid+1 to high
            sum = sum + A[j]
            if sum > right-sum
                right-sum = sum
                max-right = j

    return(max-left, max-right, left-sum + right-sum)

Since this routine traverses the whole subarray, once from mid down to low and then from mid+1 to high, it has a linear running time proportional to the length of the subarray.

Running Time = ⍬(n) where n = (high-low+1)

Now that we have got the procedure to find the maximum subarray crossing the midpoint, we can write the procedure to find the maximum subarray for A[low….high].

FIND-MAXIMUM-SUBARRAY(A, low, high)
    
    if high==low
        return (low, high, A[low])
    else 
        mid = ⌊(low + high) / 2⌋
        (left-low, left-high, left-sum) = FIND-MAXIMUM-SUBARRAY(A,     low, mid)
        (righ-low, right-high, right-sum) = FIND-MAXIMUM-SUBARRAY(A, mid+1, high)
        (cross-low, cross-high, cross-sum) = FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high)

        if left-sum >= right-sum and left-sum >= cross-sum
            return (left-low, left-high, left-sum)
        elseif right-sum >= left-sum and right-sum >= cross-sum
            return (right-low, right-high, right-sum)
        else
            return (cross-low, cross-high, cross-sum)

In the above pseudo-code we can see that maximum subarray in the left subarray and the right subarray are found out by making recursive calls to the same function i.e FIND-MAXIMUM-SUBARRAY by reducing the size of the subarray. We replace high with **mid **hence reducing the size by half. This is because they are the smaller instances of the same problem for finding maximum subarray. The maximum subarrays in left subarray and the right subarray are found out and their sums are stored in left-sum and right-sum along with their indices. The maximum subarray crossing the midpoint mid is found out by making the call to the **FIND-MAX-CROSSING-SUBARRAY procedure **that we previously wrote. At last, we find out the maximum value of the sums(left-sum, right-sum, cross-sum) from these three calls which is the value of the sum of the maximum subarray. The function returns the value of the sum along with the indices. The initial call that we will have to make is **FIND-MAXIMUM-SUBARRAY(A, 1, 16) **for the above example that we are using.

Now let’s see whether we made some improvement over the Brute Force solution which had a running time of ⍬(n²).

Analysis of the Divide and Conquer algorithm

We have already seen what recurrences are. Let’s write the recurrence for the above algorithm.

T(1) = ⍬(1) when n=1,

T(n) = 2T(n/2) + ⍬(n) when n > 1.

The base case is when we have only 1 element in the subarray(n=1). In this case, the values of high and low are equal and there is no recursion. When the value of n > 1, we need to break it down into smaller subarrays whose sizes are exactly half of the original subarray. So, if we denote the running time for this algorithm as T(n), the running time for the problem of size n/2 can be written as T(n/2). And since there are exactly two subproblems of size n/2, we have **2T(n/2) **in the above equation. The additional ⍬(n) in the equation is because we are calling **FIND-MAX-CROSSING-SUBARRAY with **total number of elements equal to n.

We will solve this recurrence using Recursion tree method as mentioned earlier.

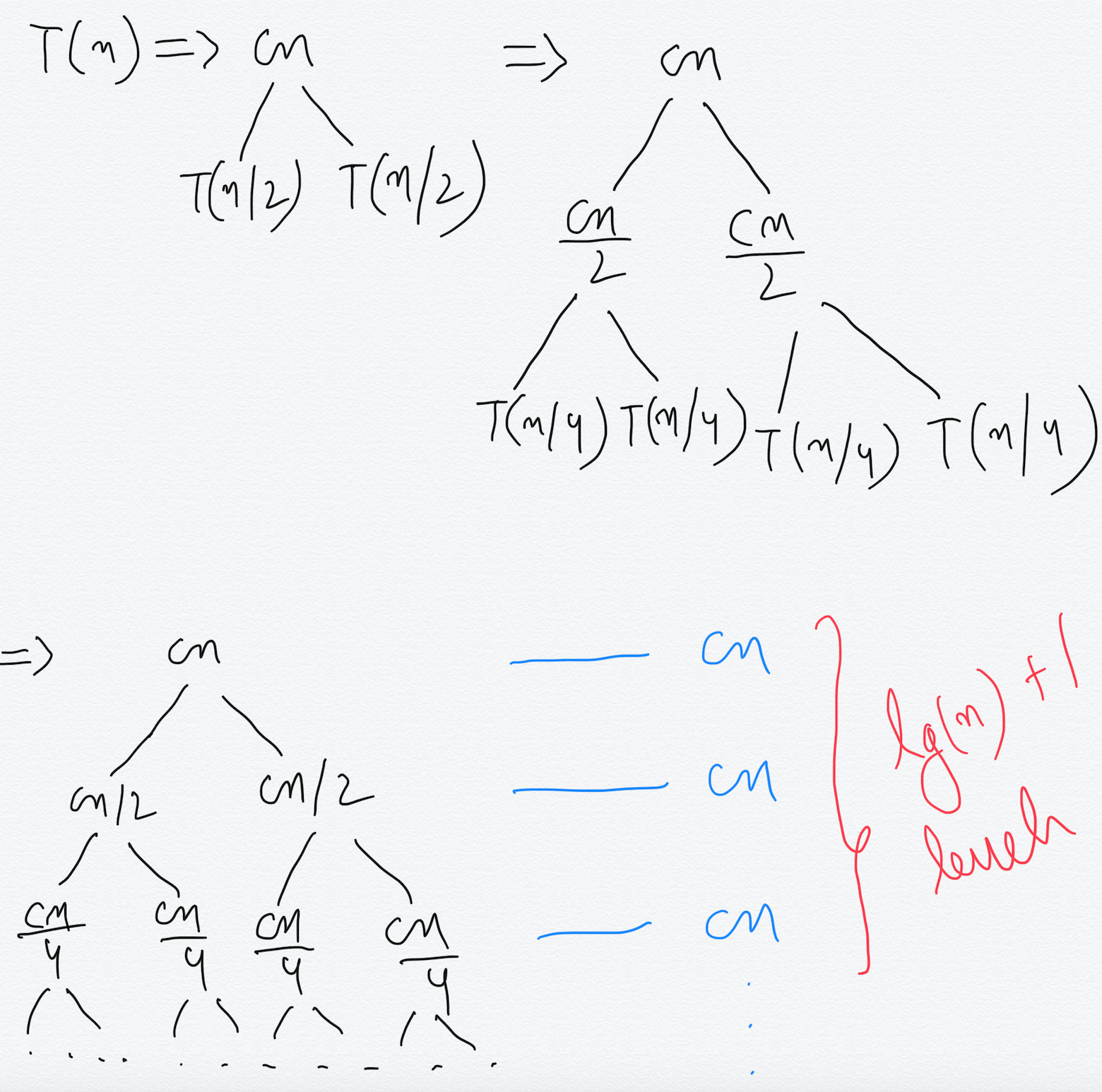
We have written ⍬(n) as (cn) as it is proportional to n and c is a constant. At each level of the recursion tree, we break down the value of T(k) as **2T(k) + ck **which was there in the recurrence. Here, k is the size of the subproblem of size k. From the above figure we can easily see that sum at each level of the recursion tree is **(cn)** and there are **lg(n)+1 **levels because at level lg(n) the size of the problem becomes 1 which is the base case.

By adding the sum at each level we get,

T(n) = cn * (lg(n) + 1) which is ⍬(n*lg(n)).

T(n) = ⍬(n*lg(n))

This is asymptotically faster than the Brute force algorithm which has a running time of ⍬(n²). Hence, we see that by using Divide and Conquer technique for the same problem, we reduced the running time significantly.

In fact, there is a linear time algorithm for finding a maximum subarray with a running time of ⍬(n) which is much faster than the above algorithms we discussed. You can try solving this problem on your own.

I hope you enjoyed reading this article. Kindly share and keep reading. Thanks!